▶ 최근점 점의 쌍을 찾는 문제?
최근접 점의 쌍(Closest Pair)을 찾는 문제는 2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제입니다.
바로 그 문제를 해결하기 위한 방법은 효율적인 분할 정복을 이용하는 것입니다.
n개의 점을 1/2로 분할하여 각각의 부분 문제에서 최근접 쌍을 찾고, 2개의 부분 해 중에서 짧은 거리를 가진 점의 쌍을 일단 찾습니다.

여기서 주의할 점!
취합할 때 중간 영역을 고려해야합니다. 이게 무슨 말이냐면, 분할된 왼쪽 점 중에 하나, 오른쪽 점 중에 하나가 최근접점 쌍이 될 수 있습니다. 그래서 중간 영역도 왼쪽 부분과 오른쪽 부분의 최단 거리인 10과 15중에 더 짧은 거리 10이내에 있는 각각 왼쪽과 오른쪽 점들만 거리 계산을 해줍니다.

▶ 최근점 점의 쌍 수도코드
ClosestPair(S)
입력: x-좌표의 오름차순으로 정렬된 배열 S에 있는 i개의 점. 단, 각 점은 (x, y)로 표현
출력: S에 있는 점들 중 최근접 점의 쌍의 거리
1. if (i <= 3) return (2또는 3개의 점들 사이의 최근접 쌍)
2. 정렬된 S를 같은 크기의 SL과 SR로 분할한다. |S|(S의 크기)가 홀수이면 |SL| = |SR| + 1이 되도록 분할
3. CPL = ClosestPair(SL) //CPL은 SL에서의 최근접 점의 쌍
4. CPR = ClosestPair(SR) //CPR은 SR에서의 최근접 점의 쌍
5. d = min{ dist(CPL), dist(CPR) }일 때, 중간 영역에 속하는 점들 중에서 최근접 점의 쌍을 찾아서 이를 CPC라고 하자. 단, dist는 두 점 사이의 거리
6. return (CPL, CPC, CPR 중에서 거리가 가장 짧은 쌍)
1. 점의 개수가 3개 이하면 분할하는 것보다 직접 계산하는 게 빨라서 직접 계산합니다.
5. 왼쪽 그룹의 최근접점 쌍의 거리와 오른쪽 그룹의 최근접점 쌍의 거리를 비교해서 더 작은 쪽값이 d가 됩니다.
또 이 d를 이용해 d이내에 있는 중간 영역의 점들의 거리를 계산합니다.
▶ 최근점 점의 쌍 수행과정
먼저 x좌표를 기준으로 정렬된 점 배열 S를 분할합니다.
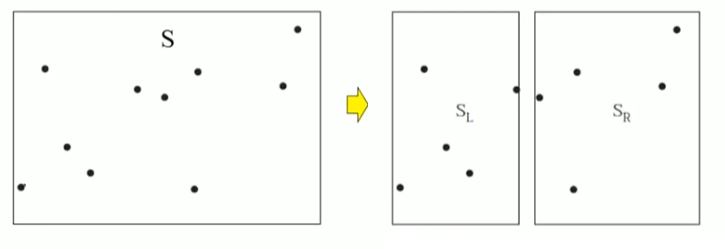
분할된 왼쪽 부분부터 ClosestPair(SL)을 호출합니다.

이제 왼쪽부분도 다시 1/2로 분할합니다.

이 부분에서도 ClosestPair(SL) 과 ClosestPair(SR)을 호출합니다. SL과 SR의 점의 개수가 3개 이하이므로 바로 이제 더 이상 함수를 호출하지 않고, 최근접점의 쌍의 거리를 구합니다. dist(CPL) = 20, dist(CPR) = 25
20과 25중 더 작은 거리인 20을 기준으로 중간 영역에 있는 점들의 최근접 점 쌍의 거리를 또 구합니다.
dist(CPC) = 10

여기까지가 맨 처음에 분할했던 왼쪽 부분의 최근접점 쌍의 거리를 구하는 과정이었습니다.
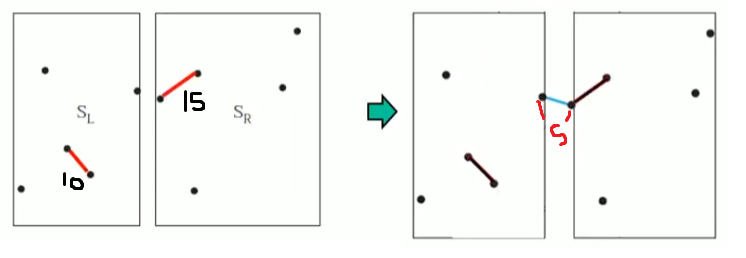
이제 똑같은 과정을 거쳐 오른쪽 부분의 최근접점 쌍의 거리를 구하면 15가 나오고, 이제 처음에 분할했던 중간 부분의 최근점점 쌍의 거리를 구합니다. 이때, dist(CPL) = 10, dist(CPR) = 15, 둘 중 더 작은 10을 기준으로 중간 영역에 있는 최근접점 쌍의 거리를 구하면 5가 나옵니다.
최종적으로 최근접점 쌍의 거리는 5입니다.
▶ 최근점 점의 쌍 파이썬 코드
import math
import copy
class Point():
def __init__(self, x, y):
self.x = x
self.y = y
def dist(p1, p2):
return math.sqrt((p1.x - p2.x) *
(p1.x - p2.x) +
(p1.y - p2.y) *
(p1.y - p2.y))
def bruteForce(P, n):
min_val = float('inf')
for i in range(n):
for j in range(i + 1, n):
if dist(P[i], P[j]) < min_val:
min_val = dist(P[i], P[j])
return min_val
def stripClosest(strip, size, d):
min_val = d
for i in range(size):
j = i + 1
while j < size and (strip[j].y -
strip[i].y) < min_val:
min_val = dist(strip[i], strip[j])
j += 1
return min_val
def closestUtil(P, Q, n):
if n <= 3:
return bruteForce(P, n)
mid = n // 2
midPoint = P[mid]
Pl = P[:mid]
Pr = P[mid:]
dl = closestUtil(Pl, Q, mid)
dr = closestUtil(Pr, Q, n - mid)
d = min(dl, dr)
stripP = []
stripQ = []
lr = Pl + Pr
for i in range(n):
if abs(lr[i].x - midPoint.x) < d:
stripP.append(lr[i])
if abs(Q[i].x - midPoint.x) < d:
stripQ.append(Q[i])
stripP.sort(key = lambda point: point.y) #<-- REQUIRED
min_a = min(d, stripClosest(stripP, len(stripP), d))
min_b = min(d, stripClosest(stripQ, len(stripQ), d))
return min(min_a,min_b)
def closest(P, n):
P.sort(key = lambda point: point.x)
Q = copy.deepcopy(P)
Q.sort(key = lambda point: point.y)
return closestUtil(P, Q, n)
P = [Point(2, 3), Point(12, 30),
Point(40, 50), Point(5, 1),
Point(12, 10), Point(3, 4)]
n = len(P)
print("The smallest distance is",
closest(P, n))
▶ 최근점 점의 쌍 시간복잡도
- S에 n개의 점이 있으면 전처리과정으로서 S의 점을 x-좌표로 정렬: O(nlogn)
- S에 3개의 점이 있는 경우에 3번, 2개의 점이면 1번 거리 계산이 필요: O(1)
- 정렬된 S를 SL과 SR로 분할하는데, 이미 배열에 정렬되어 있으므로, 배열의 중간 인덱스로 분할: O(1)
※ 중간 영역 최근접 점 쌍 찾기
아까 중간 영역을 거리가 d이내인 주변의 점들 사이의 거리를 각각 계산하기 위하여 y-좌표 기준으로 정렬합니다.
왜냐하면 그 중간 영역에 있는 점의 거리를 다 계산할 수 없는 노릇이니, 아래에서 위로 각 점을 기준으로 거리가 d이내인 주변의 점들 사이의 거리를 각각 계산하며, 최소 거리를 d로 갱신하면서 최근접 점의 쌍을 찾습니다.
y-좌표로 정렬하는데 O(nlogn) 시간이 걸리고, 아래에서 위로 올라가며 각 점에서 주변의 점들 사이의 거리를 계산하는데 O(1)시간이 걸립니다.(각 점과 거리 계산해야 하는 주변 점들의 수는 O(1)개이기 때문)
- 3개의 점의 쌍 중에서 가장 짧은 거리를 가진 점의 쌍을 리턴: O(1)
ClosestPair 알고리즘에서는 해를 취합하여 올라가는 과정에서 O(nlogn) 시간이 필요합니다. (중간 영역의 점 계산으로 인해)
k층까지 분할된 후, 층별로 수행되는 취합 과정에서 각 층의 수행 시간은 O(nlogn), 여기에 층 수인 logn을 곱하면 최종 시간복잡도인 O(nlog^2n) 을 얻을 수 있습니다.

▶ 분할 정복 적용에 주의할 점
- 분할 정복이 부적절한 경우
입력이 분할될 때마다 분할된 부분 문제의 입력 크기의 합이 분할되기 전의 입력 크기보다 커지는 경우
→ n번째의 피보나치 수를 구하기
F(n) = F(n-1) + F(n-2)로 정의되므로 순환 호출을 사용하는 것이 자연스러워 보이나, 이 경우의 입력은 1개이지만, 사실상 n의 값 자체가 입력 크기인 것입니다.
2개의 부부 문제인 F(n-1)과 F(n-2)의 입력크기는 (n-1) + (n+2) = (2n- 3)이 되어서, 분할 후 입력 크기는 거의 2배로 증가합니다.
오타나 오류 지적은 언제든 환영입니다. :)
'Algorithm > Divide-and-Conquer' 카테고리의 다른 글
| [ 알고리즘 공부 ] 선택 문제 알고리즘(Selection) (feat.python 파이썬) (0) | 2021.10.07 |
|---|---|
| [ 알고리즘 공부 ] 퀵정렬 퀵소트(Quick Sort) - 분할 정복 알고리즘(feat. python 파이썬) (0) | 2021.10.06 |
| [ 알고리즘 공부 ] 합병 정렬(Merge Sort) 알고리즘 - 분할 정복 알고리즘(python, 파이썬) (2) | 2021.10.01 |


