앞서 Boyer-Moore 알고리즘에 사용되는 두 원리 중 Bad Character 원리를 살펴 보았다.
이번에는 그 나머지 원리인 Good Suffix 원리를 배워보려고 한다.
2021.07.26 - [Algorithm/Pattern Searching] - [알고리즘 공부] Boyer-Moore Algorithm(문자열 검색 알고리즘)(1)
[알고리즘 공부] Boyer-Moore Algorithm(문자열 검색 알고리즘)(1)
Boyer-Moore 알고리즘 또한 앞서 봤던 KMP 알고리즘과 같이 문자열을 검색할 때, 패턴을 둘 이상 이동할 수 있도록 패턴에 대한 사전 처리를 진행합니다. ↓그 전 KMP 알고리즘 관련 글 2021.07.23 - [Algori
bblackscene21.tistory.com
Good Suffix 원리란?
이 원리도 Bad Character 원리와 같이 패턴의 마지막 문자부터 비교하는 것(오른쪽에서 왼쪽으로)이 특징이고,
3가지 경우에 따라 패턴을 다르게 이동합니다.
※ t: 패턴의 일부분과 일치하는 텍스트의 부분 문자열
1) 텍스트의 t가 패턴의 다른 위치에도 존재할 때
2) 텍스트에서 t의 접미사와 일치하는 패턴의 접두사가 존재할 때
3) 위 두 가지 경우가 아닐 때
1) 의 경우

→ t (노란색)는 T[3~4] = "AB" 이고, P[1~2]에도 일치하는 부분(보라색 배경)이 존재합니다.
따라서 패턴을 두 칸 이동합니다.
이 1)의 규칙은 보이어 무어 알고리즘을 위한 약한 규칙이라 별로 효과적이진 않습니다.
밑에서 더 효과적인 Strong Good Suffix 규칙에 대해 알아보겠습니다.
2)의 경우

→ t는 T[2~4] = "BAB" 이고, t의 접미사 "AB" 와 일치하는 P의 접두사 "AB"(P[0~1])가 존재합니다.
따라서 패턴을 3칸 이동합니다.
3) 의 경우

→ t는 T[3~4] 이지만, 패턴의 다른 위치에서 t와 일치하는 부분은 없습니다.
텍스트 인덱스 4 이전에는 패턴과 일치할 수 없을 것입니다. 따라서 패턴을 인덱스 4 다음으로 이동합니다.
Strong Good Suffix
1)의 경우를 보완한 대체 방법입니다.

→ P[7~8] = "AC" 와 t가 일치하다가 P[6] 에서 불일치가 발생했습니다. 불일치 글자인 "C" 를 편의상 c 라고 부르겠습니다.
앞서 살펴봤던 1)의 경우에서는 t와 일치한 문자열이 패턴의 다른 위치에 존재하면 다른 조건을 따지지 않고, 이에 따라 패턴을 이동했습니다. 하지만 Strong Good Suffix 원리에서는 1)의 경우보다 하나의 조건을 더 따집니다.
1)의 경우와 같이 따진다면 P[4~5]가 t와 일치하므로, P[4~5]를 T[7~8]위치로 이동했을 것입니다. 하지만 P[4~5]의 앞글자가 c와 같은 글자라, 앞서 했던 검사와 다를 바가 없습니다.
Strong Good Suffix는 이를 보완해서, 텍스트의 t와 일치한 문자열을 패턴에서 찾되, t와 일치하는 문자열 바로 앞 글자도 c와 다른지 검사한 후, 만약 다르다면 그제서야 이동합니다.
따라서 위 그림에서는 P[1~2]가 "AC"로 t와 일치하면서, 바로 앞 글자인 P[0]이 c와 다른 "A" 이므로, P[0~2]를 T[6~8]로 이동시킨 것입니다.
- Preprocess for strong good suffix rule
먼저 코드를 자세히 보기 전에, "border"에 관해 알아야 합니다.
- border란?
suffix(접미사)이며 동시에 prefix(접두사)가 될 수 있는 string을 border라고 합니다. border는 테두리, 경계라는 의미처럼단어의 앞과 뒤로 감싸고 있어서 border라는 말을 사용하는 것 같습니다.
접두사이자 접미사가 되는 border의 시작 인덱스를 저장하는 배열을 편의상 bpos라고 부르겠습니다.
"ABBABAB"로 예를 들자면,
bpos[i]
bpos[0] = 5 ▶ "ABBABAB" 의 border = "AB"
bpos[1] = 6 ▶ "BBABAB" 의 border = "B"
bpos[2] = 4 ▶ "BABAB" 의 border = "BAB"
bpos[3] = 5 ▶ "ABAB" 의 border = "AB"
bpos[4] = 6 ▶ "BAB" 의 border = "B"
bpos[5] = 7 ▶ "AB" 의 border = ""
bpos[6] = 7 ▶ "B" 의 border = ""
bpos[7] = 8 ▶ border가 존재 X
여기서 shift 배열은 shift[n] = search함수에서 j위치가 n일 때 불일치가 발생할 시 패턴을 이동시키는 횟수 (search 함수에서 보면 알겠지만, s에 더해주는 값입니다.)
예로 들었던 "ABBABAB"로 shift배열을 구한다면,
shift = {0, 0, 0, 0, 2, 0, 4, 1} // 0으로 남아 있는 것은 Preprocess for case2 함수에서 구할 것입니다.
함수에서 아래 부분은 i와 j를 함께 이동하며 가다가 불일치가 일어나게 됐을 때 처리하는 내용입니다.
만약에 이 while문 조건에 만족했을 때 j = 4, i = 2 라고 한다면, (앞서 예를 들었던 "ABBABAB")
그럼 shift[4] = 2가 됩니다.
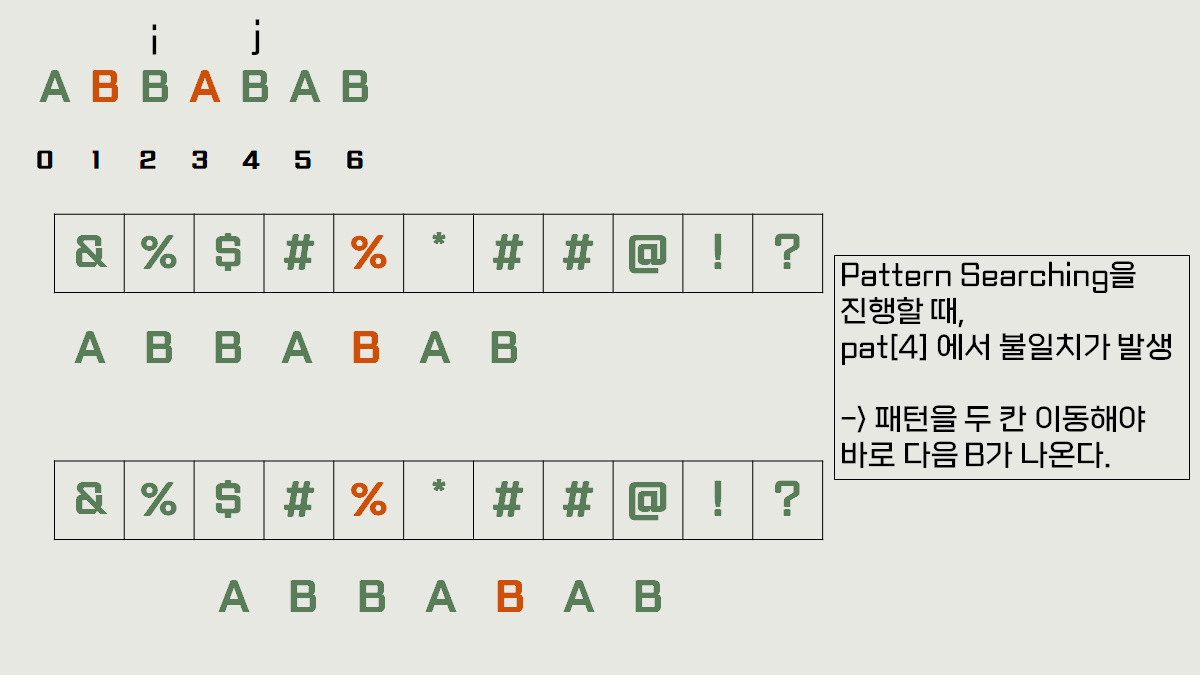
왜 pat[i], pat[j] 가 아니라 pat[i-1], pat[j-1] 일까요?
바로 strong good suffix rule 에서는 텍스트와 일치했던 패턴의 문자열의 앞글자도 신경 써서 서치를 실행하기 때문입니다. 그래서 앞글자가 다르다는 판단 후에 shift 배열을 건드리는 것입니다.
if (shift[j] == 0) 은 이미 값이 들어간 배열은 건드리지 않기 위해서 검사합니다.
while(j <= m && pat[i-1] != pat[j-1])
{
if (shift[j] == 0)
shift[j] = j-i;
j = bpos[j];
}
아래는 strong suffix rule을 위한 preprocess 함수 코드입니다.
void preprocess_strong_suffix(int *shift, int *bpos,
char *pat, int m)
{
int i = m, j = m+1;
bpos[i] = j;
while(i > 0)
{
while(j <= m && pat[i-1] != pat[j-1])
{
if (shift[j] == 0)
shift[j] = j-i;
j = bpos[j];
}
i--; j--;
bpos[i] = j;
}
}
- Preprocess for case2
case2를 위한 Preprocess 함수는 간단합니다. i를 search함수를 실행할 때, 패턴인덱스를 가리키는 변수라고 생각하면 좀 더 이해하기 쉬울 겁니다. (i = 0일 때는 패턴 문자열을 다 검사한 경우, i = 1일 때는 pat[0] 빼고 다 검사한 경우 ...)
따라서 j를 bpos[0]으로 초기화하고, i가 증가하면서 i와 j가 만나기 전까지는 shift배열의 값은 5로 지정됩니다.
(이때 접미사는 "AB")
| A | B | B | A | B | A | B |
i와 j가 만나게 되면, 접미사의 길이는 당연히 줄어듭니다. j를 bpos[j]의 값으로 변경합니다.
void preprocess_case2(int *shift, int *bpos,
char *pat, int m)
{
int i, j;
j = bpos[0];
for(i=0; i<=m; i++)
{
/* set the border position of the first character of the pattern
to all indices in array shift having shift[i] = 0 */
if(shift[i]==0)
shift[i] = j;
/* suffix becomes shorter than bpos[0], use the position of
next widest border as value of j */
if (i==j)
j = bpos[j];
}
}
j = pat 인덱스, s = pat 0 인덱스가 위치한 text 인덱스
search 함수는 별도의 설명이 없어도 이해하기에 쉬울 겁니다.
void search(char *text, char *pat)
{
// s is shift of the pattern with respect to text
int s=0, j;
int m = strlen(pat);
int n = strlen(text);
int bpos[m+1], shift[m+1];
//initialize all occurrence of shift to 0
for(int i=0;i<m+1;i++) shift[i]=0;
//do preprocessing
preprocess_strong_suffix(shift, bpos, pat, m);
preprocess_case2(shift, bpos, pat, m);
while(s <= n-m)
{
j = m-1;
/* Keep reducing index j of pattern while characters of
pattern and text are matching at this shift s*/
while(j >= 0 && pat[j] == text[s+j])
j--;
/* If the pattern is present at the current shift, then index j
will become -1 after the above loop */
if (j<0)
{
printf("pattern occurs at shift = %d\n", s);
s += shift[0];
}
else
/*pat[i] != pat[s+j] so shift the pattern
shift[j+1] times */
s += shift[j+1];
}
}
Boyer-Moore 알고리즘은 good suffix rule이나 bad character 중 하나를 선택해서 구성하는 알고리즘이 아닌, 두 원리를 동시에 사용하되 각 경우마다 두 원리가 제시하는 shift array 중 최선의 선택을 하도록 만드는 알고리즘입니다.
나중에 기회가 된다면 그 코드도 짜서 올리겠습니다.
오류나 오타 지적해주시면 감사하겠습니다. :)
'Algorithm > Pattern Searching' 카테고리의 다른 글
| [알고리즘 공부] 보이어 무어 알고리즘 Boyer-Moore Algorithm(문자열 검색 알고리즘)(1) (0) | 2021.07.26 |
|---|---|
| [알고리즘 공부] KMP Algorithm (문자열 검색 알고리즘) (1) | 2021.07.23 |

